Planar 7-Atoms Cluster
Let’s consider a simple system formed by seven atoms with Lennard-Jones (LJ) interactions in a planar space. This simple model is presented in the exercise 9 of the Plumed Masterclass 21.2. This LJ cluster has several stable isomers (Figure 1), which can be distinguished in a space of the CVs second (SCM) and third (TCM) central moments of the distribution of coordinations (orange stars in Figure 2).
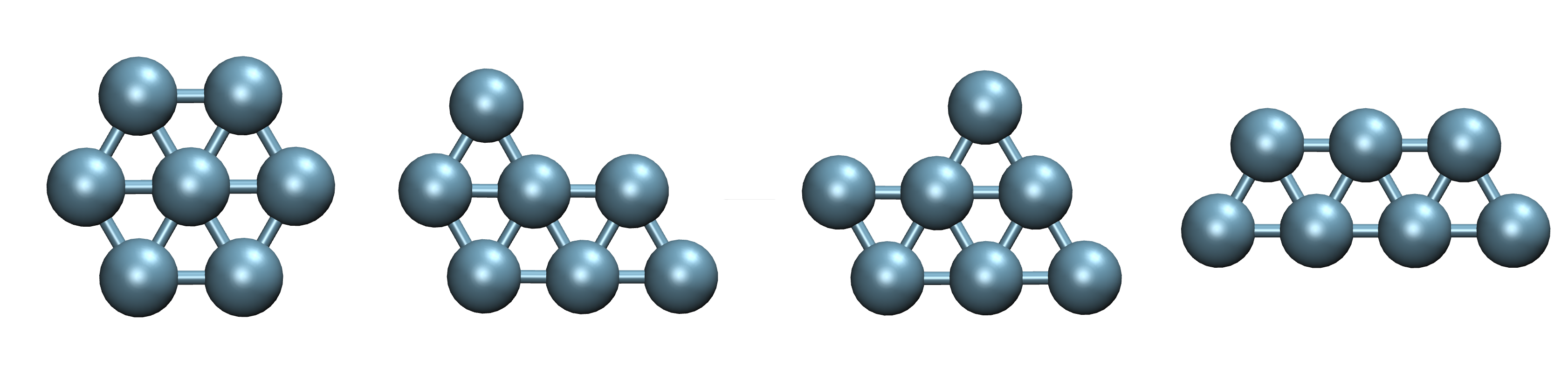
Figure 1. Local minima isomers of the LJ cluster used in this tutorial.
The n-th central moment, $\mu_n$, of the coordination number of an N-atoms cluster is defined as
\[(5)\] \[{\mu_n} = \frac{1}{N} \sum_{i=1}^{N} \left( {X}_{i} - \left< {X} \right> \right)^n ~,\]where $\left< {X} \right>$ is the mean value of $X_i$, which is the coordination of the i-th atom,
\[(6)\] \[X_i= \sum_{i\ne j}\frac{1-(r_{ij}/d)^8}{1-(r_{ij}/d)^{16}} ~,\]with $r_{ij}$ the distance between atoms $i$ and $j$, and $d$ a reference parameter. For this example, d is fixed to 1.5 $\sigma$, in LJ units.
